Points are one of the most fundamental objects of Euclidean geometry. They do not have any area or length and they are ideally not even visible. Here we are going to see point as a fundamental object for constructing geometrical objects in computer program.
Points are described with the help of X and Y coordinates (x, y). In computer graphics, points are the basic thing we have to deal with. Any object whether it is a two dimensional ( such as circle, square, rectangle ), or three dimensional (such as sphere, cone, cube ) etc, are described by a set of points through their surface. It is the collection of points that we trace to give the illusion of an object.
In three dimensional geometry a point has three coordinates (x, y, z). The point could be rotated, reflected, translated etc along with the object when translation is performed with the object.
The have written a class in java which contains the properties and basic methods that we need to simulate a point, and do most of the 3-d graphics works.
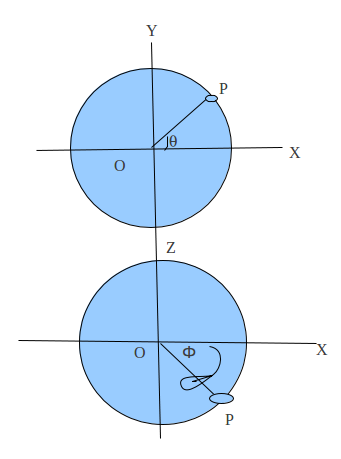
In my previous post, I have discussed about the angles (theta, phi ). Use them as a conventions for this post.
In the Next post , I will describe the complete process of actually drawing a three dimensional sphere in a frame or a window.
Points are described with the help of X and Y coordinates (x, y). In computer graphics, points are the basic thing we have to deal with. Any object whether it is a two dimensional ( such as circle, square, rectangle ), or three dimensional (such as sphere, cone, cube ) etc, are described by a set of points through their surface. It is the collection of points that we trace to give the illusion of an object.
In three dimensional geometry a point has three coordinates (x, y, z). The point could be rotated, reflected, translated etc along with the object when translation is performed with the object.
The have written a class in java which contains the properties and basic methods that we need to simulate a point, and do most of the 3-d graphics works.
/**
*
* @author Rajan Prasad Upadhyay
* class RPoint.java
*/
public class RPoint {
public double x;
public double y;
public double z;
public RPoint(){}
public RPoint(double x,double y,double z){
this.x=x;
this.y=y;
this.z=z;
}
public void viewPoint(){
System.out.println("("+x+","+y+","+z+")");
}
public int getX(){
int i=(int)Math.rint(x);
return i;
}
public int getY(){
int i=(int)Math.rint(y);
return i;
}
public int getZ(){
int i=(int)Math.rint(z);
return i;
}
public RPoint getRotateAlongTheta(int radius,double theta,RPoint center){
double tx=x-center.x,ty=y-center.y,tz=z-center.z;
double tx1,ty1,tz1;
tx1=tx*Math.cos(Math.toRadians(theta))-tz*Math.sin(Math.toRadians(theta));
tz1=tx*Math.sin(Math.toRadians(theta))+tz*Math.cos(Math.toRadians(theta));
tx=tx1+center.x;
tz=tz1+center.z;
RPoint p=new RPoint(tx,y,tz);
return p;
}
public RPoint getRotateAlongPhi(int radius,double phi, RPoint center){
double tx=x-center.x,ty=y-center.y,tz=z-center.z;
double tx1,ty1,tz1;
tx1=tx*Math.cos(Math.toRadians(phi))-tz*Math.sin(Math.toRadians(phi));
ty1=tx*Math.sin(Math.toRadians(phi))+tz*Math.cos(Math.toRadians(phi));
tx=tx1+center.x;
ty=ty1+center.y;
RPoint p=new RPoint(tx,ty,z);
return p;
}
//unit vectors
public double getL(){
double a=x/Math.sqrt(x*x+y*y+z*z);
return a;
}
public double getM(){
double a=y/Math.sqrt(x*x+y*y+z*z);
return a;
}
public double getN(){
double a=z/Math.sqrt(x*x+y*y+z*z);
return a;
}
//project coordiantes functions
public int getViewX(int cz){
int a=(int)Math.rint(cz*x/z);
return a;
}
public int getViewY(int cz){
int a=(int)Math.rint((cz)*y/z);
return a;
}
public int getViewZ(int cz){
int a=(cz);
return a;
}
//3d translations functions
public RPoint translate( RPoint p){
RPoint a=new RPoint(x-p.x,y=p.y,z-p.z);
return a;
}
public RPoint inverseTranslate( RPoint p){
RPoint a=new RPoint(x+p.x,y+p.y,z+p.z);
return a;
}
public void RotateAlongTheta( double theta, RPoint center){
double tx=(x-center.x)*Math.cos(Math.toRadians(theta))-(z-center.z)*Math.sin(Math.toRadians(theta));
double tz=(x-center.x)*Math.sin(Math.toRadians(theta))+(z-center.z)*Math.cos(Math.toRadians(theta));
x=tx+center.x;
z=tz+center.z;
}
public void RotateAlongPhi( double phi, RPoint center){
double tz=(z-center.z)*Math.cos(Math.toRadians(-phi))-(y-center.y)*Math.sin(Math.toRadians(-phi));
double ty=(z-center.z)*Math.sin(Math.toRadians(-phi))+(y-center.y)*Math.cos(Math.toRadians(-phi));
y=ty+center.y;
z=tz+center.z;
}
public RPoint RotateAlongX(int theta, RPoint center){
//x does not change
double tz=(z-center.z)*Math.cos(Math.toRadians(-theta))-(y-center.y)*Math.sin(Math.toRadians(-theta));
double ty=(z-center.z)*Math.sin(Math.toRadians(-theta))+(y-center.y)*Math.cos(Math.toRadians(-theta));
return new RPoint(x,ty+center.y,tz+center.z);
}
public RPoint RotateAlongY( int theta, RPoint center){
//ie rotating along y axix , clockwise
double tx=(x-center.x)*Math.cos(Math.toRadians(theta))-(z-center.z)*Math.sin(Math.toRadians(theta));
double tz=(x-center.x)*Math.sin(Math.toRadians(theta))+(z-center.z)*Math.cos(Math.toRadians(theta));
return new RPoint(tx+center.x,y,tz+center.z);
}
public RPoint RotateAlongZ(int theta, RPoint center){
//z constant
double tx=(x-center.x)*Math.cos(Math.toRadians(theta))-(y-center.y)*Math.sin(Math.toRadians(theta));
double ty=(x-center.x)*Math.sin(Math.toRadians(theta))+(y-center.y)*Math.cos(Math.toRadians(theta));
return new RPoint(tx+center.x,ty+center.y,z);
}
//prospective view coordinate giving functions
public void RevolveAlongY(double theta, RPoint sample){
double tx=(x-sample.x)*Math.cos(Math.toRadians(theta))-(z-sample.z)*Math.sin(Math.toRadians(theta));
double tz=(x-sample.x)*Math.sin(Math.toRadians(theta))+(z-sample.z)*Math.cos(Math.toRadians(theta));
x=tx+sample.x;
z=tz+sample.z;
}
public void RevolveAlongX(double theta, RPoint sample){
}
public RPoint getPerspective( RPoint viewPoint){
double xp=x-(-z)/(viewPoint.z-z)*(x-viewPoint.x);
double yp=y-(-z)/(viewPoint.z-z)*(y-viewPoint.y);
double zp=0;
return new RPoint(xp,yp,zp);
}
public RPoint rotateAlongY(double angle){
double x2=x*Math.cos(Math.toRadians(angle))-z*Math.sin(Math.toRadians(angle));
double y2=x*Math.sin(Math.toRadians(angle))+z*Math.cos(Math.toRadians(angle));
return new RPoint(x2,y2,z);
}
}
In my previous post, I have discussed about the angles (theta, phi ). Use them as a conventions for this post.
In the Next post , I will describe the complete process of actually drawing a three dimensional sphere in a frame or a window.