The 3D sphere Drawing in a computer program

The 3D sphere

The three dimensional sphere can be made by modeling the sphere in the spherical coordinate system.

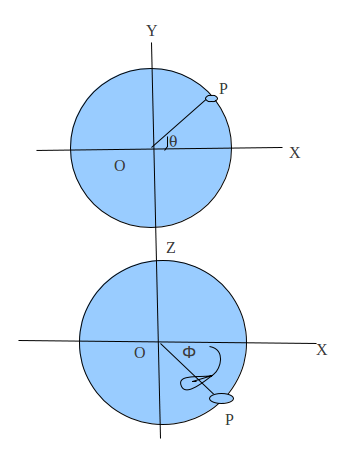
As the sphere is a three dimensional object, it could not be pictorially shown in a single picture. So it is important to view the sphere or any three dimensional object from two different dimensions which is exactly done in the above picture.

Imagine a shpere and place it in the origin of a three dimensional cartesian-coordinate-system.
 Now view of the sphere from the front is exactly same as the top picture and from the top is same as the second picture. Here ‘p’ is a variable point we are dealing with and OP is an imaginary line joining the center of sphere with the point p. Here theta ‘ q‘ is the angle made in the front view between line ‘OP’ and ‘OX’ and phi ‘ Ф‘ is the angle made by the line ‘OP’ with the ‘OX’ in the top view.(Actually in three dimensional imagination, these are the angles made by the axis with the projection of line ‘OP’ on the planes XY and XZ). Now thinking as a scientist, we can say that the surface of the sphere can be generated if we vary the point p from top to bottom (ie theta<=90 and theta>=-90) and from right to left and again to right (ie phi>=0 and phi<=360 degrees). We could not take the continuous collections of point , but the picture would be smoother if we took the interval as small as possible.

You should be smart enough to generate the formula to calculate the collection of points p by yourself. I would be in terms of the radius of the sphere multiplied by some trigonometric expressions of theta and phi and may have some arithmetic signs such as plus or minus.

CREATING THREE DIMENSIONAL VIEW

The formula, I assumed you have generated from the above model, should generate points and these points drawn simply in the monitor would produce simple two dimensional effect of the sphere. What I am concerned in this section is techniques like projection(parallel, oblique, perspective) that will give a real three dimensional impression of sphere. In simplest words, just make a function that would return a projected point of a real point and pass all the points of your sphere through that function. The returned point will be more three dimensional.

Ok before that, lets discuss about the formula, from the projected diagrams, we can say that the coordinate x depends on both the angles. The coordinate y depends only on theta, and the z-coordinate depends only on phi. We store all the points in a two dimensional matrix lets say points. Now the formula would be

points.x[i][j]=r.cos(theta).cos(phi)

points.y[i][j]=r.sin(theta)

points.z[i][j]=r.sin(phi)

running these formulas in the loop would produce the points. After the matrix is being generated, joining the points of the rows together will produce the latitudes of the sphere and joining the points of a column together will produce the longitudes. You need lots of calculations and stages for the generated points to be passed through before you could really create an actual and real looking sphere. Some of the key terms you should learn are-: shadow rendering or mapping techniques, rotation of points, translation. Symmetric properties of sphere could help reduce your initial calculations. You should choose the actual coordinate of your system, the viewing plane, and the point of intersection of the rays of light in case of prospective projection (which is the most realistic projection). This is the figure of final sphere we are going to draw.

Click Here to view the next post where I comprehend the general theories of point and its operations.
Source code for this sphere.